LeetCode-53.最大连续子序列和(Maximum Subarray) 题解
Leetcode-53(力扣-53)
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
题目描述
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
个人题解
class Solution:
def maxSubArray(self, nums: list) -> int:
gbl, local = [nums[0]], [nums[0]]
if len(nums) == 1:
return nums[0]
for i in range(1, len(nums)):
local.append(max(nums[i], nums[i] + local[i - 1]))
gbl.append(max(gbl[i - 1], local[i]))
return gbl[-1]
个人题解分析
设定数组nums的长度为L,gbl[i]存储nums中从0到i的的最大连续子数组和,0<=i<=L-1。
利用DP的思想,遍历nums数组,分析gbl[i]和gbl[i-1]的关系,即可求出最终的gbl[L-1]的结果。
首先分析gbl[i]的场景:
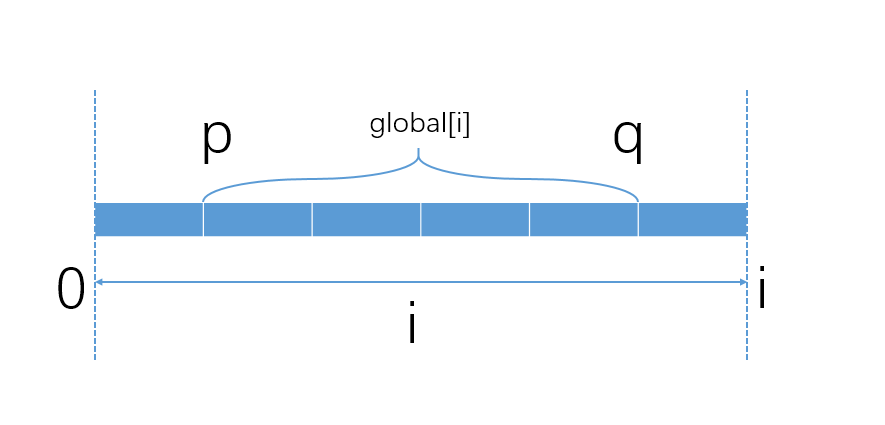
当遍历到i时,gbl[i]存储的当前最大连续子数组和,其子数组边界为p和q,0<=p<=q<=i,公式如下:
gbl[i] = $\sum_{k=p}^q nums[k]$
然后分析gbl[i+1]的场景:
当遍历到nums[i+1],如果出现了比gbl[i]大的连续数组必然会包括nums[i+1],因为如果出现比gbl[i]大的连续数组和不包括nums[i+1],gbl[i]已经是当前最大值。那么包含nums[i+1]的最大连续数组和有2种场景:
- global[i+1] = nums[i+1]。该连续数组只包括nums[i+1]
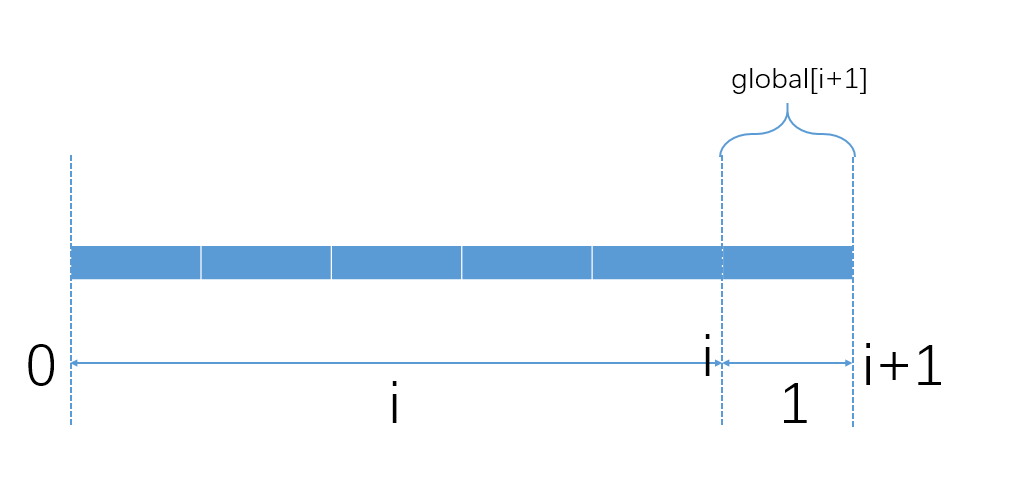
-
该连续数组不仅只包括nums[i+1]。也就是说,除了包括nums[i+1]以外,在0到i中,存在一个m(0<=m<=i)到i的连续数组。那么global[i+1]可以看成是由2段组成: 从m到i和i+1。
global[i+1]=$\sum_{k=m}^i nums[k]$ +nums[i+1]
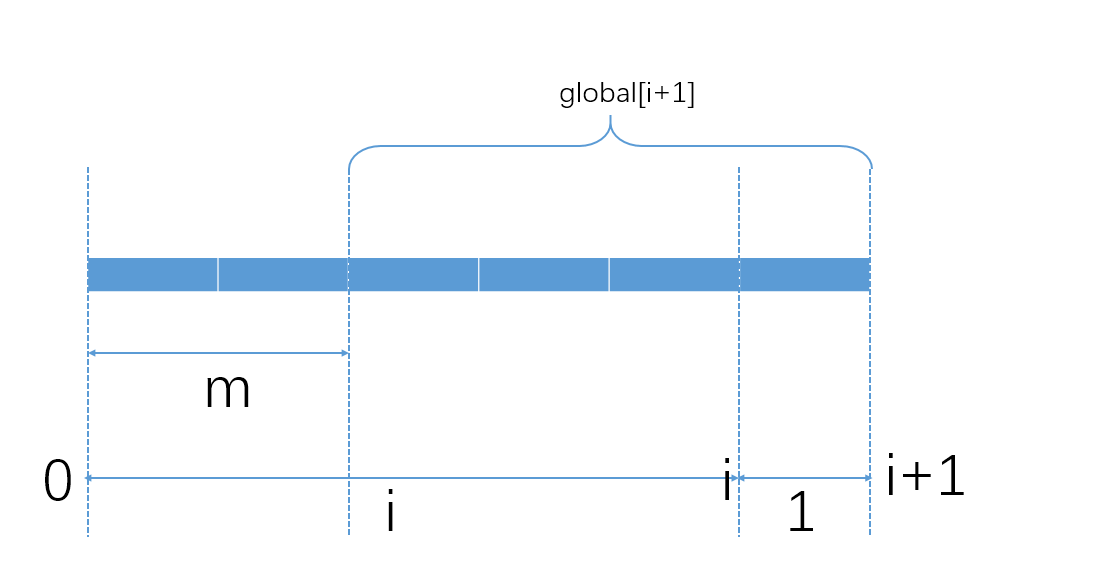
2段中nums[i+1]的值是固定的,需要在包含nums[i]的连续数组中找出最大值。此时,同样可以利用DP的思想,建立数组local[],从0到L进行遍历, local[i]表示包含nums[i]的连续数组的最大值,称之为局部最大值或者边界最大值。
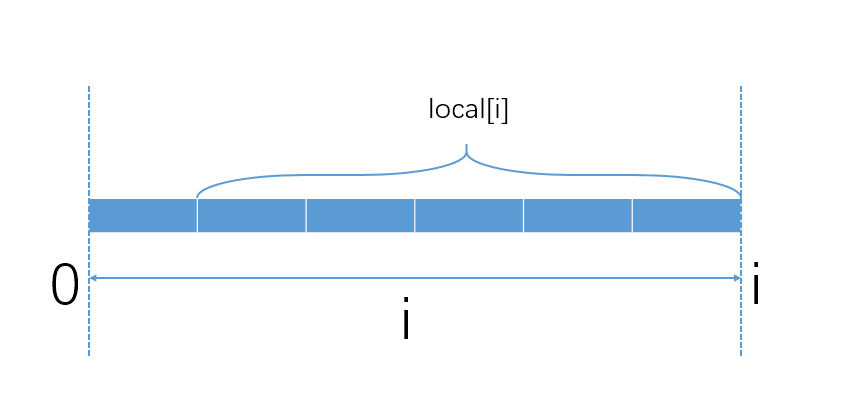
那么分析local[i+1]和local[i]关系时,自然可以用公式local[i+1] = MAX(nums[i+1], local[i]+nums[i+1] ),之前计算global[i+1] 就可以用以下的递归公式了:
gbl[i+1] = local[i]+nums[i+1]
最后,gbl[i+1]需要取2种场景下大的: global[i+1] = MAX(nums[i+1], nums[i+1]+local[i])
最后gbl[L-1]即为所有的解。