LeetCode-959.由斜杠划分区域(Regions Cut By Slashes) 题解
Leetcode-959(力扣-959)
In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a /, \, or blank space. These characters divide the square into contiguous regions.
(Note that backslash characters are escaped, so a \ is represented as "\\".)
Return the number of regions.
Example 1:
Input:
[
" /",
"/ "
]
Output: 2
Explanation: The 2x2 grid is as follows:
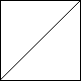
Example 2:
Input:
[
" /",
" "
]
Output: 1
Explanation: The 2x2 grid is as follows:
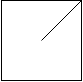
Example 3:
Input:
[
"\\/",
"/\\"
]
Output: 4
Explanation: (Recall that because \ characters are escaped, "\\/" refers to \/, and "/\\" refers to /\.)
The 2x2 grid is as follows:
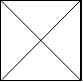
Example 4:
Input:
[
"/\\",
"\\/"
]
Output: 5
Explanation: (Recall that because \ characters are escaped, "/\\" refers to /\, and "\\/" refers to \/.)
The 2x2 grid is as follows:
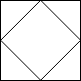
Example 5:
Input:
[
"//",
"/ "
]
Output: 3
Explanation: The 2x2 grid is as follows:
Note:
1 <= grid.length == grid[0].length <= 30grid[i][j]is either'/','\', or' '.
题目描述
给定一个N * N的二维数组,数组中的元素由空格,/和\构成,由这些元素可以将二维数组分隔成不同的区域,参见5个例子。求被分隔的区域数量。
优秀题解
def regionsBySlashes(self, grid):
f = {}
def find(x): #找出集合中的某一个元素,来代表整个集合
f.setdefault(x, x)
if x != f[x]:
f[x] = find(f[x])
return f[x]
def union(x, y): #合并集合
f[find(x)] = find(y)
for i in xrange(len(grid)):
for j in xrange(len(grid)):
if i:
union((i - 1, j, 2), (i, j, 0)) #合并上下元素
if j:
union((i, j - 1, 1), (i, j, 3)) #合并左右元素
if grid[i][j] != "/": #合并"\"和空白区域内的0,1和2,3区域
union((i, j, 0), (i, j, 1))
union((i, j, 2), (i, j, 3))
if grid[i][j] != "\\": #合并"/"和空白区域内的3,0和1,2区域
union((i, j, 3), (i, j, 0))
union((i, j, 1), (i, j, 2))
return len(set(map(find, f)))
优秀题解分析:
由于在该题的话题区域里看到了Union-Find的话题,所以找到了一位大神刚好用到此算法,现在分析该大神的算法代码。参见此处。关于Union-Find的的介绍在《算法导论》的21章有介绍。
首先,作者将数组的一个元素,也就是一个最小的方格分成4个区域,如图:
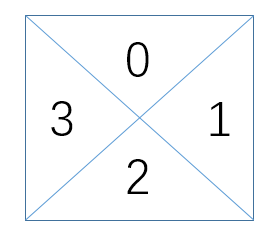
可以发现对于,空格、/、\三种情况,0、1、2、3的连通情况分别是:
- 空格:所有区域都连通
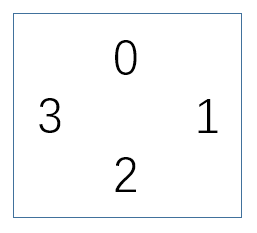
/: 0和3连通,1和2连通

\: 0和1连通,2和3连通
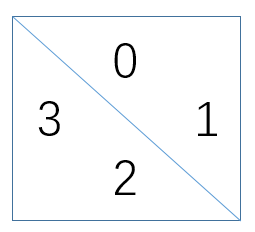
题目即可转化成图中共有多少个连通的区域。
其次,也可以很明显得看出来,划分出区域以后。每一个数组元素的相邻的左右,和上下间的关系:
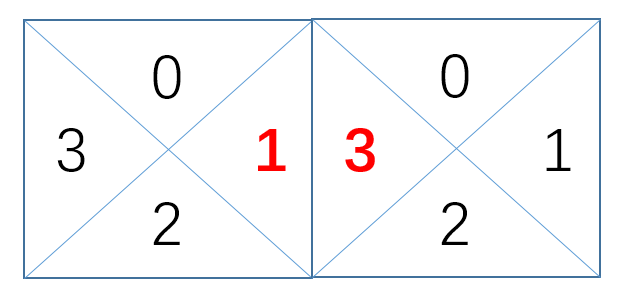
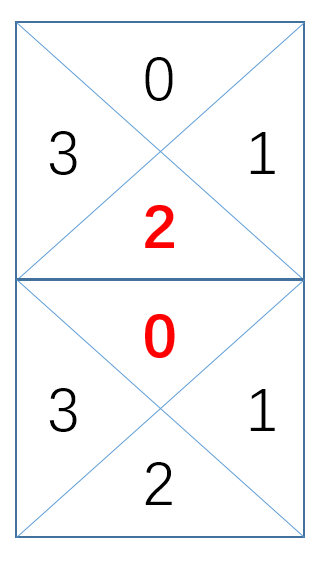
左右的1和3区域是相通的,上下的0和2区域是相通的。
最后,通过2层for循环遍历二维数组,分别对上述的三种情形进行合并操作。最终求解。
需要值得一提的是,作者的union和find函数:
在Union-Find算法中,union函数用于将2个集合合并,find函数用于返回合并后的集合中的某一个元素来代表该集合。
本算法中,利用dict来实现union函和find函数。如有2个区域A,B,有一个字典f,那么f[A]=B,f[B]=B,令区域A和区域B均指向区域B来实现A,B两个区域的合并。
find函数分析:
f = {}
def find(x): #找出集合中的某一个元素,来代表整个集合
f.setdefault(x, x)
if x != f[x]:
f[x] = find(f[x])
return f[x]
该函数的输入为一个元组,元组前2个元素代表区域所在的坐标位置,第3个元素代表区域本身的代号,即0到3中的一个。输出为该区域所指向的区域。函数会在字典f查询所指向的区域,如果不是指向自己,就会递归调用find函数,直到找到一个区域是指向自己 ,该区域便能代表能连通到该区域的所有集合。如以下的dict:
(0, 0, 0) = {tuple: 3} (0, 0, 1)
(0, 0, 1) = {tuple: 3} (0, 0, 1)
(0, 0, 2) = {tuple: 3} (0, 0, 1)
(0, 0, 3) = {tuple: 3} (0, 0, 1)
用第0行0列的区域1来代表,第0行0列的1,2,3,4这四个区域,说明1,2,3,4这四个区域是连通的。
union函数分析:
def union(x, y): #合并集合
f[find(x)] = find(y)
union函数表明用x区域所在的集合在指向y区域所在的集合,从而将x区域所在的集合跟y区域所在的集合合并。由于x和y本身是最小的区域单位,通过find函数找到x区域和y区域所在的集合 。